1 范数、2 范数、无穷范数的通俗理解?
Excerpt 引言 很多人学完了矩阵理论或者数值分析,脑海里还是蒙的,有些比较基础的东西至今还没有一个深刻的理解,就比如矩阵理论中1范数、2范数,以及无穷范数代表什么含义呢? 范数的理解 我们来讲个故事,保证大家能够…
引言
很多人学完了矩阵理论或者数值分析,脑海里还是蒙的,有些比较基础的东西至今还没有一个深刻的理解,就比如矩阵理论中1范数、2范数,以及无穷范数代表什么含义呢?
范数的理解
我们来讲个故事,保证大家能够明白,这里主要是以向量范数为例。假设小花要选男朋友,她想在小强和小刚之间选。
第1种情况,小花的选择标准只有一个,即身高。
那么,小强的身高是1.7米,小刚的身高是1.8米,所以她会选小刚(这里假如女孩子喜欢高一点的男孩子)。
第2种情况,小花的择偶标准有两个,即身高和月收入。
假如小强的月收入为2万,小刚为1万。那么在小花的眼中,小强={1.7,2},小刚={1.8,1}。
可是,这怎么比呢?
于是,小花想出了一个办法,更方便度量,就是综合收入和身高的平均值,她的办法是画出坐标系,看最终谁的点离原点点更远。
所以通过勾股定理,可以求得小强更远,所以她选择了小强。
换句话也就是说,范数可以等于点到坐标零点的距离。
是不是很清新,是不是很明了?
所以通俗的说,范数就是为了方便度量而定义出的一个概念,主要就是面对复杂空间和多维数组时,选取出一个统一的量化标准,以方便度量和比较。请务必记住,范数是人为定义的一种度量方法。
那么,如果一个向量里元素更多。例如,小花的择偶标准里再加上性格评分,以及身体素质评分,就变成了(1.7, 2.0, 4.0, 5.8 )这样形式的向量,维度又增加了。
所以,我们还可以定义更多的统一度量标准。
1范数、2范数、无穷范数(向量范数)
这三种不同的范数都是不同的度量方法。
(0范数,向量中非零元素的个数,这里不解释)
1范数:所有元素绝对值的和。
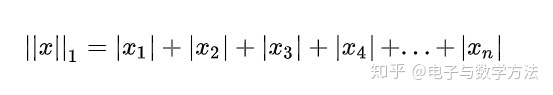
2范数:所有元素平方和的开方。
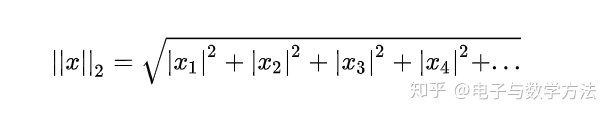
无穷范数:正无穷范数:所有元素中绝对值最小的。负无穷范数:所有元素中绝对值最大的。
║x║∞=max(│x1│,│x2│,…,│xn│)
《武林外传》里一段台词用来解释这几个范数或许是最生动的了。
佟湘玉有一天在同福客栈说:“额滴神呐,展堂,你说隔壁的赛貂蝉有什么好。”
老白:“她没没你温柔,没你贤惠,没你大气,没你端庄。”
佟湘玉:“那为啥你们总往她那跑呢?”老白:“因为他的相貌是满分啊”。
看到没有?
如果用2范数来衡量赛貂蝉和佟湘玉,那么可以说佟湘玉并不占下风,但是压不住人家赛貂蝉有一个满分啊,也就是说,从无穷范数的角度来看,赛貂蝉的稳稳超过佟湘玉的。
再看一个辩题“当今社会更需要通才还是专才”。通才是1范数2范数比较大,而专才就是无穷范数比较大。
是不是一下子就整明白了,最后,记住,范数是比较向量/矩阵是否“优秀”的一种标准而已。为了加深印象大家还可以使用MATLAB去编程计算一下。
最后我们讲一下范数对于数学的意义,范数其实就是从数学本质上描述了“什么叫空间”,它不再是我们日常生活对话里的“空间”了。它从更深刻的角度来洞察我们这个世界,下次你一看到空间,你一给你家装修,搞空间艺术,你是不是马上就会想到,我们搞的是范数2空间。
我们可以想象一下会不会在那么一个平行宇宙,那里的人搞空间艺术,要考虑的却是范数3的空间呢?
 絢香猫
絢香猫