✖️ 叉乘
标签
数学
知识领域/数学
数学/叉乘
计算机/计算机图形学
知识领域/计算机图形学
数学/向量
数学/矩阵
字数
321 字
阅读时间
2 分钟
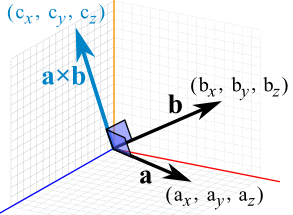
点乘被用于向量和一维矩阵的计算,叉乘的计算结果c是一个新的向量。
几何意义
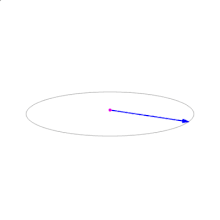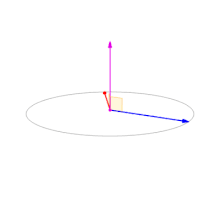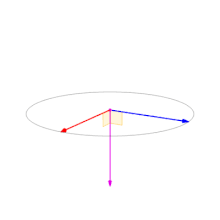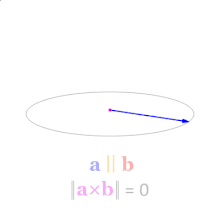
- 两个向量的叉积
c与这两个向量组成的坐标平面垂直,c向量长度在两个向量平行时为零。 - 因为叉乘的反交换律:“
” 所以可以通过 c向量的方向来判断b向量是在a的左边还是右边。
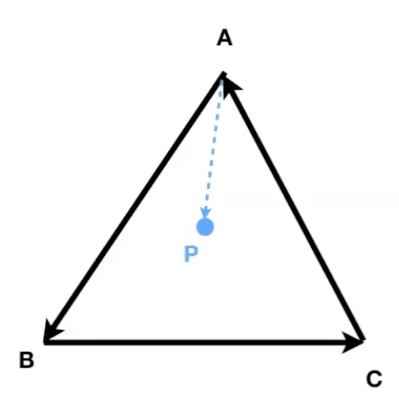
- 假设有一点
P和一个三角形,通过遍历三角形所有边并叉乘点P的相对位置,还可以得出点P是在三角形的内侧还是外侧。
使用右手定则确定叉乘结果向量的方向
这两种方法都可以,第一种更好记一些。
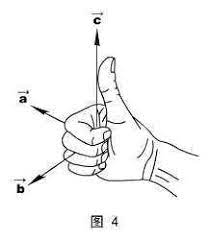
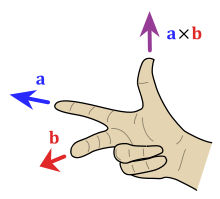
计算方法
代码实现
typescript
export function crossProduct(vA: number[], vB: number[]) {
const product = (t = 0, v = 0) => t * v
const itemCrossProduct = (mA: number[], mB: number[]) => {
return mA.reduce(product) - mB.reduce(product)
}
return [
itemCrossProduct([vA[1], vB[2]], [vA[2], vB[1]]),
itemCrossProduct([vA[2], vB[0]], [vA[0], vB[2]]),
itemCrossProduct([vA[0], vB[1]], [vA[1], vB[0]]),
]
}参考资料
- https://www.shuxuele.com/algebra/vectors-cross-product.html
- https://zh.wikipedia.org/wiki/%E5%8F%89%E7%A7%AF
 絢香猫
絢香猫 絢香音
絢香音