向量范数和矩阵范数
两个标量我们可以比较大小,比如 1,2,我们知道 2 比 1 大。但是现在如果是两个向量 ,,我们如何比较大小呢?此时我们把一个向量通过不同的方法,映射到一个标量,从而可以比较大小,这个标量学名就叫做“范数”。
范数分为向量范数和矩阵范数。
向量 。
import numpy as np
X = np.array([-2, 5, 0, -3, 4])
# X 为 [-2 5 0 -3 4]为 x 向量各个元素绝对值 次方和的 次方。
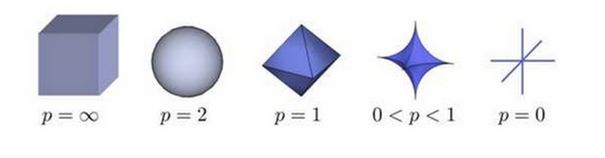
上图表示了 p 从无穷到 0 变化时,三维空间中到原点的距离(范数)为 1 的点构成的图形的变化情况。
# 向量 p-范数
def norm_p(X, p):
return (sum([abs(x)**p for x in X])) ** (1.0/p)
norm_p(X, 1) # p 取 1,结果为 14.0
norm_p(X, 2) # p 取 2,结果为 7.348
norm_p(X, 3) # p 取 3,结果为 6.073特殊地,当 取 0,1,2,,,时,对应范数意义如下。
- 向量 0-范数:向量中非零元素的个数。
# 向量零范数
def norm_0(X):
return sum([1 for x in X if x])
norm_0(X)
# X 的零范数为 4向量 1-范数: 向量中各个元素绝对值之和。
# 向量 1-范数
def norm_1(X):
return sum([abs(x) for x in X])
norm_1(X)
# X 的 1-范数为 14向量 2-范数: 向量中各个元素平方和的 次方,L2 范数又称 Euclidean 范数(欧几里得范数),也就是通常说的向量长度。
# 向量 2-范数
def norm_2(X):
return (sum([x*x for x in X])) ** (1.0/2)
norm_2(X)
# X 的 2-范数为 7.348向量 -范数:向量的正无穷范数即向量元素绝对值中的最大值。到原点的最远距离。
# 向量无穷-范数
def norm_inf(X):
return max([abs(x) for x in X])
norm_inf(X)
# X 的无穷-范数为 5向量 -范数:向量的负无穷范数即向量元素绝对值中的最小值。到原点的最近距离。
# 向量负无穷-范数
def norm_finf(X):
return min([abs(x) for x in X])
norm_finf(X)
# X 的负无穷-范数为 0- 正定性:,当 时,。
- 齐次性:。
- 三角不等式:。
矩阵 。
矩阵 0-范数:标识矩阵中非零元素的个数。可以表示矩阵的稀疏程度。
矩阵 1-范数:也称列和范数,即所有矩阵列向量的绝对值之和的最大值。
矩阵 2-范数:也称谱范数,即 的最大特征值开平方。
其中, 是 矩阵的特征值,只有方阵才有 2-范数。
矩阵 -范数:矩阵的 -范数,也称行和范数,即所有矩阵行向量的绝对值之和的最大值。
矩阵 F-范数:即 Frobenius 范数,矩阵元素的平方和再开平方。
这玩意最难看懂,网上好多公式还是错的,写了代码实现。计算方法为 矩阵的最大特征值的开平方。
import numpy as np
x = np.array([-1, 1, 0](-1,%201,%200))
print x
xtx = np.matmul(x.T, x)
print 'lambda ', np.linalg.eigvals(xtx)
n2 = np.linalg.norm(x, ord = 2)
print 'norm_2 ', n2, np.sqrt(27.71086452)程序执行结果:
[[-1 1 0]
[-4 3 0]
[ 1 0 2]]
lambda [ 27.71086452 0.03392256 4.25521292]
norm_2 5.26411099011 5.2641109904712309矩阵 X 的 2-范数计算是先计算 的特征值 ,然后找 中的最大值,再开方。代码里 xtx 即为 ,eigvals 函数的返回值就是各个 。
矩阵第 m 行与第 n 列交叉位置的那个值,等于第一个矩阵第 m 行与第二个矩阵第 n 列,对应位置的每个值的乘积之和。
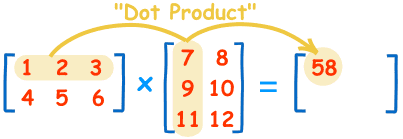
矩阵的本质就是线性方程式,两者是一一对应关系。
设 A 是 n 阶方阵,如果存在数 m 和非零 n 维列向量 x,使得 成立,则称 m 是矩阵 A 的一个特征值(characteristic value)或本征值(eigenvalue)。
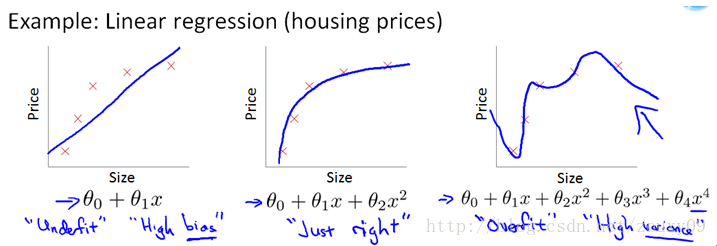
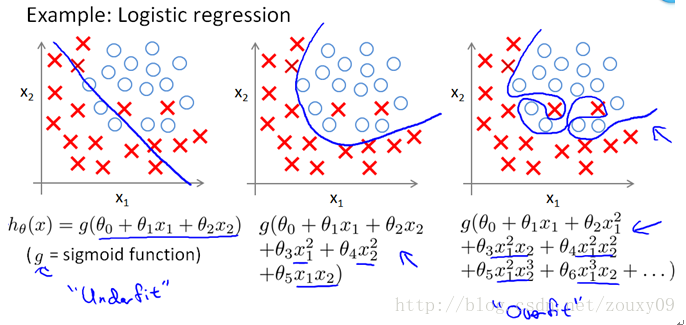
机器学习中常用 L1 范数和 L2 范数来进行正则化,因为机器学习中往往需要最小化损失函数 Loss function,而最小化 Loss function 的过程中,模型参数不加以限制就容易导致过拟合,所以我们使用 L1 范数和 L2 范数把参数向量转化成一个可以度量的标量,同时加上最小化的约束,就达到了控制模型参数的目的从而防止过拟合。
- 《动手学深度学习》
- https://ww2.mathworks.cn/help/matlab/ref/norm.html
- https://mathpix.com/图片转公式貌似要收钱
- NumPy 范数计算 | liao.cpython.org
- 理解矩阵乘法 | ruanyifeng.com阮一峰
- https://blog.csdn.net/zouxy09/article/details/24971995
 絢香猫
絢香猫